L'utilisation des calculatrices n'est pas autorisée pour cette épreuve.
On se contentera, pour les applications numériques, d'un seul chiffre significatif. On prendra

ainsi que

pour l'accélération de la pesanteur.

Catapultes

Les catapultes sont des engins mécaniques destinés à lancer de gros projectiles pour attaquer des murailles. Mais on peut généraliser cette définition à d'autres situations que le siège de fortifications : dans le monde végétal, les plantes peuvent stocker de l'énergie sous différentes formes pour la libérer rapidement et provoquer des mouvements très rapides (plantes "carnivores", éjection de graines et de spores). On peut également utiliser l'énergie électromagnétique pour fabriquer une catapulte. Nous nous intéressons ici à ces deux variantes de catapultes.
Les parties 1, 2 et 3 sont indépendantes.

1 Catapultes capillaires

Lorsqu'on fait condenser de la vapeur d'eau sur une surface très hydrophobe, on observe les phénomènes suivants : les gouttes d'eau (de taille submillimétrique) ont une forme sphérique et ne s'étalent pas sur la surface solide. La taille de chaque goutte augmente au cours du temps par la condensation de la vapeur. Lorsque deux gouttes initialement proches se touchent et coalescent en une seule goutte plus grosse, cette dernière saute verticalement (fig. 1). On cherche à analyser ce phénomène et, en particulier, à trouver la taille optimale de goutte pour la propulsion verticale.

On considère deux gouttes identiques de rayon , ayant une tension interfaciale avec l'air . Quelle est la variation d'énergie de surface résultant de la coalescence de ces deux gouttes?
En admettant qu'il n'y a pas de dissipation d'énergie lors de la coalescence et que les gouttes sont initialement au repos, quelle est la vitesse verticale initiale du mouvement de la goutte résultant de la coalescence? Quelle est la valeur numérique de pour des gouttes d'eau (masse volumique , tension de surface ) de rayon ?
Quelle est la hauteur atteinte par la goutte, si on néglige la friction dans l'air?
Immédiatement après la coalescence, la goutte est très fortement déformée par rapport à sa forme d'équilibre sphérique (fig. 1b). On cherche à estimer par un raisonnement en loi d'échelle le temps caractéristique de déformation de la goutte. En comparant l'énergie de surface de la goutte et l'énergie

Figure 1 - En haut : saut d'une goutte d'eau résultant de la coalescence de deux gouttes sur un substrat superhydrophobe. L'intervalle entre images est

et le diamètre de la goutte éjectée est

. Images tirées de Boreyko & Chen, Phys. Rev. Lett. 103, 184501 (2009). En bas : Simulation numérique montrant l'évolution de la forme de la goutte immédiatement après coalescence. Figure tirée de S. Farokhirad, J. Morris & T. Lee, Phys. Fluids 27, 102102 (2015).

cinétique liée aux mouvements internes du liquide, montrer que ce temps caractéristique

est tel que :

. Dans ce raisonnement, on ignorera tous les préfacteurs numériques. Quel est l'ordre de grandeur de ce temps pour une goutte d'eau millimétrique?
5. Dans un écoulement, la puissance dissipée par unité de volume du fait de la viscosité est

où

est la viscosité dynamique,

est la composante

du vecteur vitesse et

la composante

de la coordonnée d'espace. On suppose ici que tous les termes

sont du même ordre de grandeur. Montrer, toujours en ignorant les préfacteurs numériques, que l'énergie dissipée par viscosité à l'intérieur de la goutte pendant sa déformation est proportionnelle à

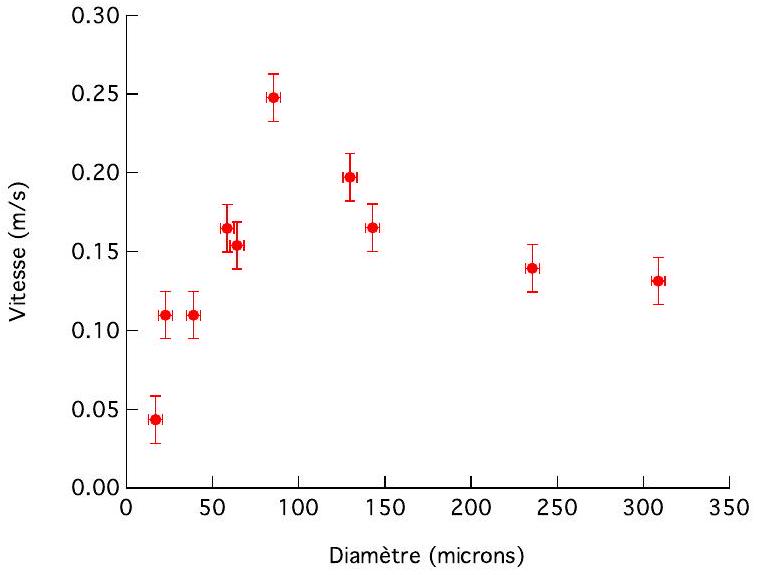
Figure 2 - Vitesse verticale initiale de la goutte après coalescence en fonction du diamètre moyen (après coalescence) des gouttes. Données tirées de Boreyko & Chen, Phys. Rev. Lett. 103, 184501 (2009).

Il y a en fait un préfacteur numérique important pour l'énergie dissipée qui est :
. En faisant un bilan d'énergie prenant en compte la dissipation visqueuse, déterminer l'évolution de la vitesse d'éjection verticale de la goutte en fonction du rayon et des paramètres physiques du problème. est ici le rayon de la goutte après coalescence. Y a-t-il une valeur du rayon pour laquelle la vitesse d'éjection est maximale? Si oui, quelle est elle? Quelle est alors la vitesse d'éjection? Comment se comparent ces résultats aux données expérimentales de la fig. 2 ?
La viscosité dynamique de l'eau est : Pa.s.

2 Application à l'éjection des spores de champignons

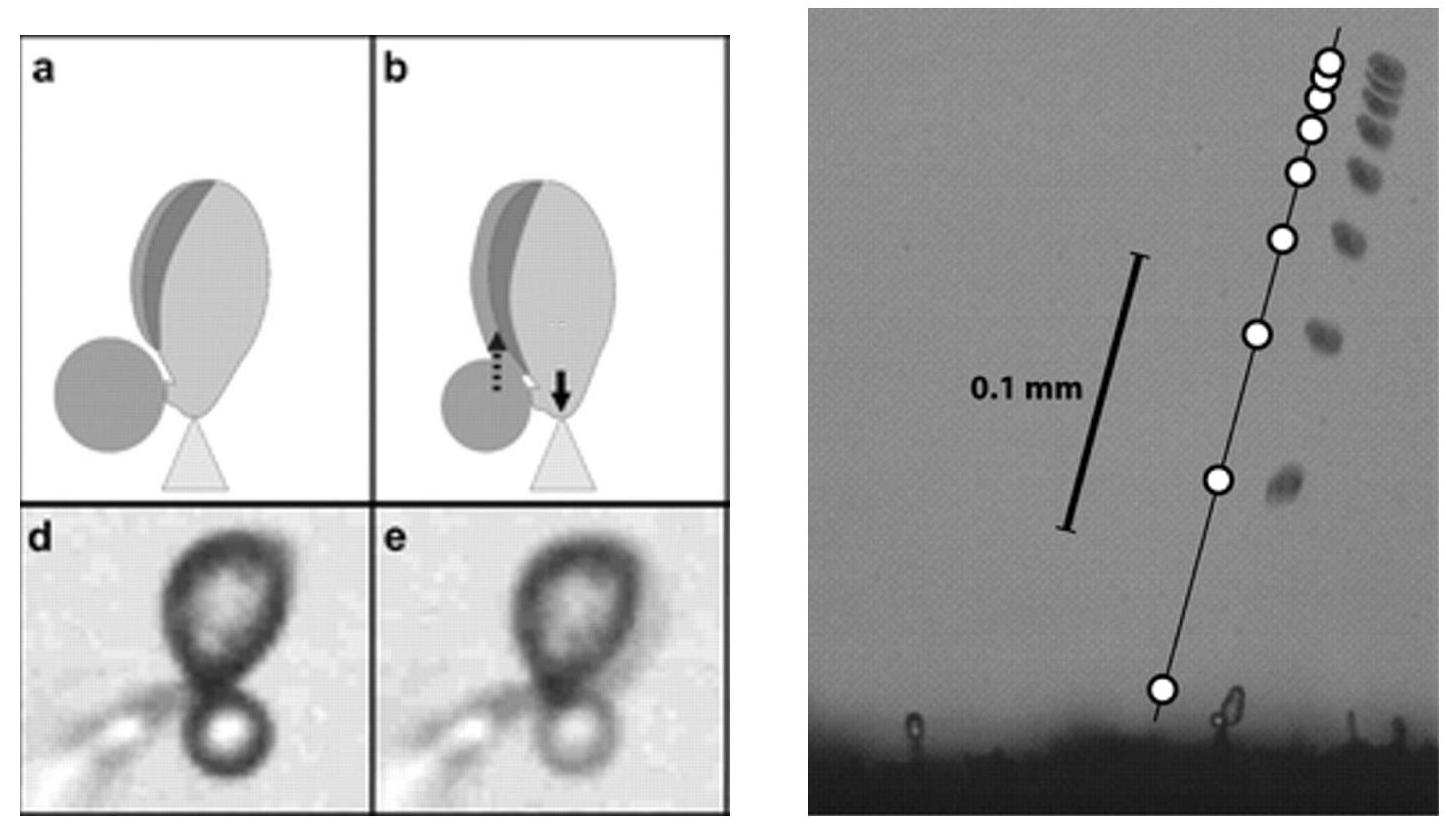
Figure 3 - Éjection d'une spore de champignon. À gauche, a, b : schéma de la coalescence de la goutte d'eau (en gris foncé) sur la spore. d, e : deux vues de la coalescence prises avec une caméra ultra-rapide (largeur des images :

). À droite, surimpression des positions d'une spore à des intervalles de temps de

. Images tirées de A. Pringle et al., "The captured launch of a ballistospore", Mycologia, 97, 866 (2005).

Certaines espèces de champignons ont développé une stratégie efficace pour éjecter les spores depuis les lamelles situées sous le chapeau. À la base du support de la spore se trouve une petite zone hydrophile qui permet la croissance d'une goutte d'eau (fig. 3). Lorsque la goutte d'eau, de rayon

est assez grande, elle fusionne avec une très mince couche d'eau couvrant la surface de la spore et s'étale à son tour en une couche mince couvrant toujours la surface entière de la spore. Le rayon de la spore, que l'on supposera sphérique,

est de l'ordre de

, sa masse

est de l'ordre de

.
7. Estimer la variation d'aire interfaciale eau/air et la variation d'énergie interfaciale associée. On supposera que le film d'eau initialement présent couvre la totalité de la surface de la spore et que le rayon de la goutte d'eau est deux fois plus petit que celui de la spore.
8. En admettant que la variation d'énergie interfaciale est intégralement récupérée en énergie cinétique, estimer la vitesse initiale d'éjection de la spore et comparer cette vitesse à celle observée expérimentalement.
9. Quel est le nombre de Reynolds associé à l'écoulement d'air autour de la spore ? La viscosité dynamique de l'air est

Pa.s et sa masse volumique est

.
10. En déduire l'expression de la force de traînée exercée par l'air sur la spore en mouvement en fonction notamment du rayon de la spore et de sa vitesse.
11. La gravité joue-t-elle un rôle dans le mouvement? Si la spore est éjectée horizontalement, décrire sa trajectoire et donner en particulier la longueur et le temps de freinage. Comparer votre prédiction au mouvement réel représenté sur la fig. 3.

3 Catapultes électromagnétiques

On considère une catapulte électromagnétique constituée de deux rails en aluminium parallèles de section carrée (de côté

) et de longueur

, reliés d'une part à une extrémité à un générateur G (un groupe de condensateurs) en série avec un interrupteur

et d'autre part à un rail mobile de longueur

et de masse

(de matériau et section identiques aux deux rails parallèles et perpendiculaire à ceux-ci), comme schématisé sur la figure 4 . On suppose que le rail mobile se déplace sans frottement dans la direction

entre les deux rails parallèles et assure un contact électrique parfait au niveau de chaque rail. Le rail mobile est de plus muni d'un support de masse négligeable (non représenté sur le schéma) permettant de pousser un projectile de masse M.

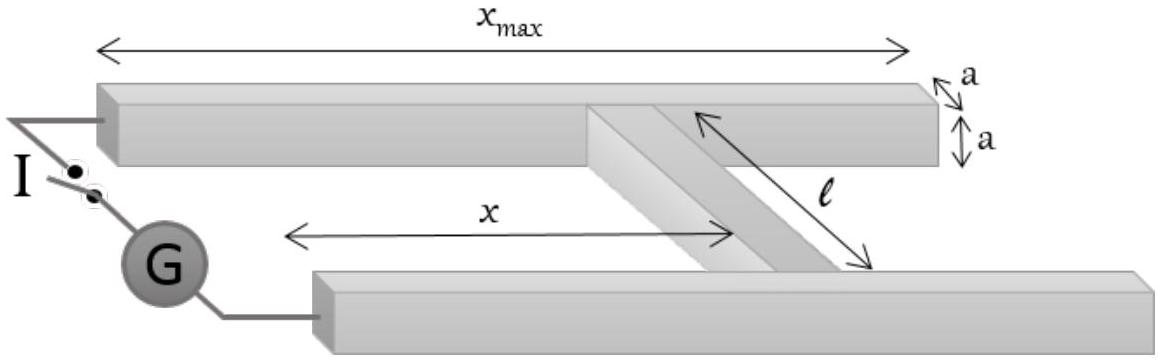
Figure 4 - Schéma de la catapulte

Lors de la fermeture de l'interrupteur

, le groupe de condensateurs initialement chargé fournit de l'énergie au circuit, en particulier sous forme d'énergie cinétique fournie à la partie mobile (d'où le nom de catapulte électromagnétique).

On considère le circuit dans l'approximation des régimes quasi-stationnaires. Le groupe de condensateurs est équivalent à un condensateur de capacité notée

. On note

l'inductance propre du circuit lorsque le conducteur mobile se trouve à la position

(voir figure 4). L'ensemble des parties résistives du système est assimilable à une résistance

en série avec la capacité

et l'inductance

. On note

l'intensité dans le circuit.
12. Rappeler l'expression de l'énergie magnétique à l'instant

d'un circuit d'inductance

parcouru par un courant d'intensité

, ainsi que la force électromotrice s'exerçant sur un circuit déformable. En effectuant de deux manières un bilan de la puissance fournie par la source au circuit, montrer que le module de la force exercée sur la partie mobile s'écrit :

Faire un schéma montrant la direction du champ magnétique dans le plan situé à égale distance des deux conducteurs parallèles ainsi que la direction de la force agissant sur la partie mobile.
13. La figure 5 indique quelques valeurs de

pour différentes valeurs de

et pour quelques valeurs de

. Expliquer pourquoi

varie en bonne approximation linéairement en fonction de la distance

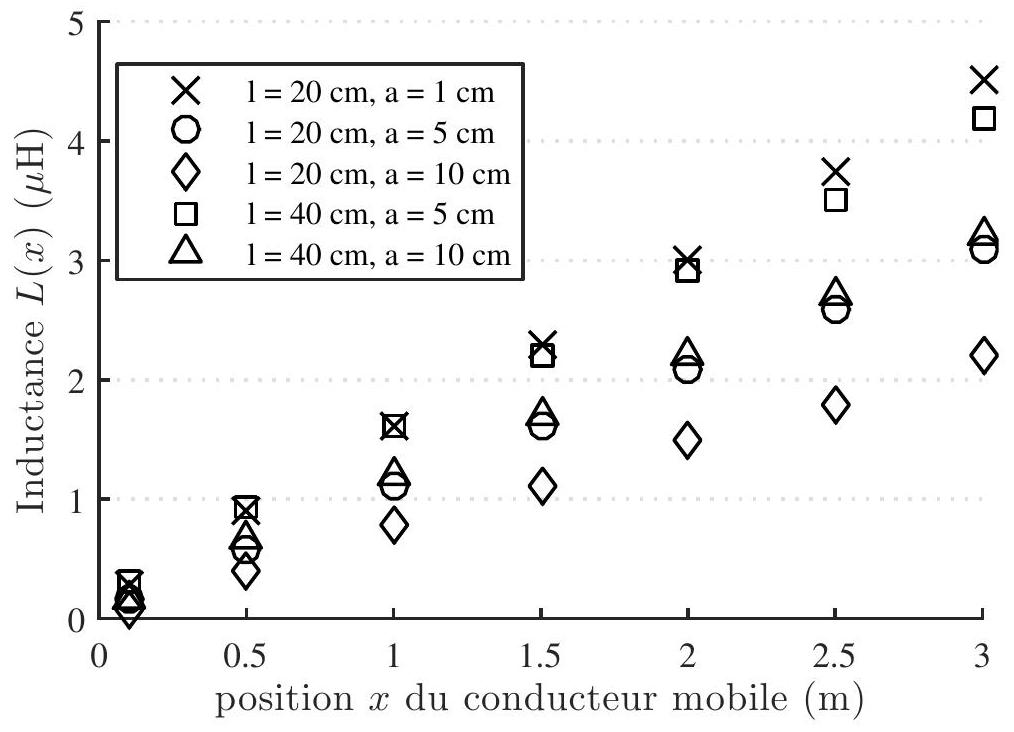
Figure 5 - Valeur de l'autoinductance

du circuit constituant la catapulte en fonction de la distance

, pour diverses valeurs des paramètres géométriques

dans l'hypothèse où

est grand devant l'écart

entre les deux barres parallèles. On notera

, valeur qui sera dans toute la suite de l'énoncé supposée constante.
14. En supposant que le plan de la catapulte est incliné d'un angle

par rapport à l'horizontale, et en supposant un courant constant de valeur

dans le circuit, établir la relation littérale entre

et la vitesse

de la partie mobile de masse

après un parcours de longueur

, et une position initiale en

.
15. Déduire à partir de la figure 5 les valeurs des paramètres géométriques

(parmi ceux proposés) qui vont minimiser le courant requis pour atteindre une vitesse donnée. On suppose dans toute la suite que

sont fixées à ces valeurs.
16. Déterminer un ordre de grandeur du courant

(toujours supposé constant) nécessaire pour catapulter un ballon de football, de masse

avec une catapulte de longueur

, pour les paramètres géométriques de conducteur mobile les plus favorables déterminés à la question précédente. La masse volumique de l'aluminium est

. Dans toute la suite, la longueur

de la catapulte est fixée à 1 m .
17. En déduire une ordre de grandeur de la charge nécessaire à la production d'un tel courant pendant le catapultage.
18. Dans ce qui précède, on a supposé que le courant était constant pour l'estimation des ordres de grandeur. En réalité, le courant est initialement nul avant la fermeture de l'interrupteur, et ne peut donc être constant lors du fonctionnement de la catapulte. Le groupe de condensateur de capacité équivalente

est initialement chargé avec une charge notée

. Rappeler l'équation différentielle qui régit le courant

.
On suppose l'inégalité suivante vérifiée :

Interpréter cette inégalité en précisant le sens de chacun des termes, et déduire une description en deux phases du fonctionnement de la catapulte une fois l'interrupteur fermé.
19. Dans le cadre de l'inégalité précédente, établir l'équation approchée décrivant l'évolution temporelle du courant dans le circuit pendant la phase de catapultage correspondant à la décharge du groupe de condensateurs, en supposant constante la résistance totale

du circuit.

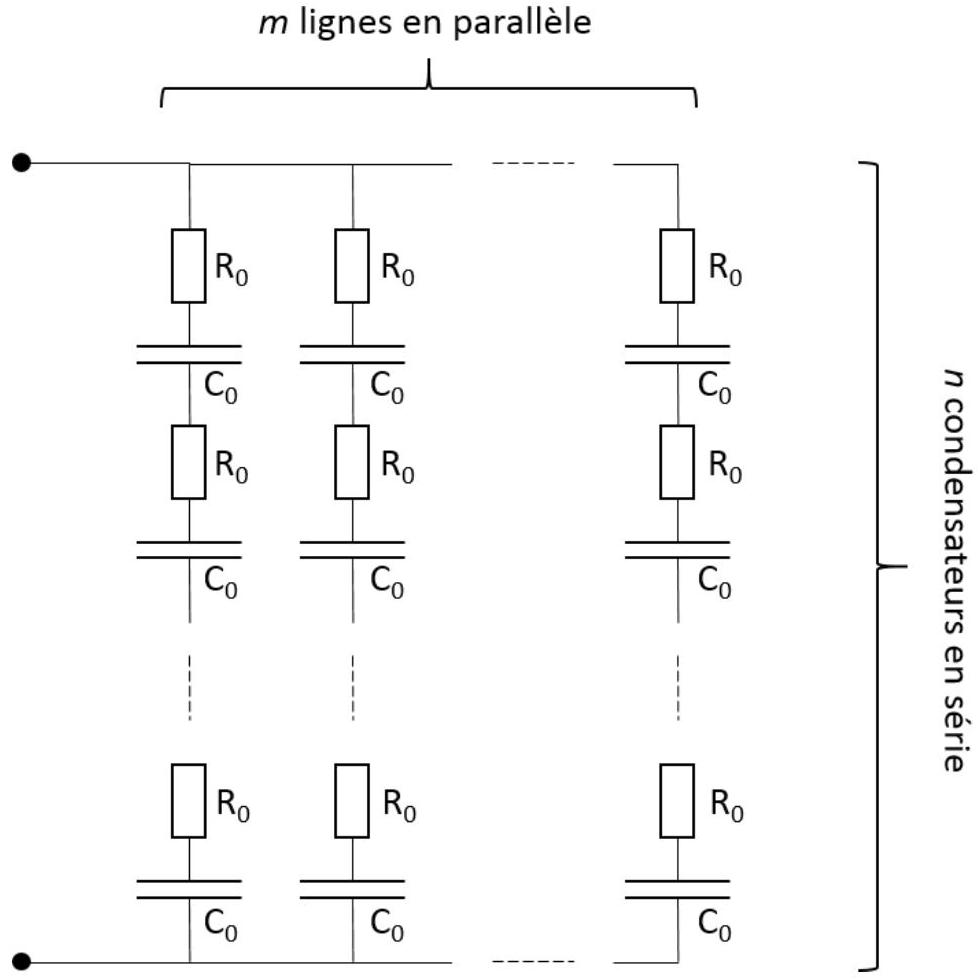
Figure 6 - Association de

condensateurs formant le générateur

de la catapulte électromagnétique.

On peut trouver sur le marché des condensateurs de très forte valeur de capacité (plusieurs milliers de Farads), mais limités à des tensions de charge relativement basses (quelques Volts). Ces condensateurs présentent en général également des pertes, modélisables par une résistance de perte associée en série avec la partie capacitive. On considère un groupement de condensateurs associés comme sur la figure 6. Etablir les valeurs de capacité et de résistance équivalentes à un tel groupe de condensateurs dans une représentation ( ) en série, ainsi que la charge maximale que peut fournir le groupe de condensateurs et la tension correspondante à laquelle on doit le soumettre pour le charger.
En supposant négligeable la résistance liée aux rails en aluminium, établir en fonction de , et l'expression du courant de décharge dans le circuit. Avec et , montrer que et permet de fournir un courant d'intensité et de temps caractéristique de décharge compatibles avec toutes les hypothèses effectuées et les valeurs numériques trouvées dans les questions précédentes. La conductivité électrique de l'aluminium vaut .
Estimer un ordre de grandeur de l'élévation de température dans les rails d'aluminium pendant la durée utile de la projection. La capacité thermique de l'Aluminium vaut .
Estimer l'efficacité de la catapulte en comparant l'énergie "utile" aux autres formes d'énergie mises en jeu. Quel peut être alors l'intérêt de ce genre de dispositif de projection en pratique?